Recently, both through grading proofs and trying to teach some new math majors how to write proofs, I’ve had the opportunity to see a lot of invalid proofs. I want to record here some of the more common errors that invalidate an argument here.
Compilation errors. When grading a huge stack of problem sets, I kind of feel like a compiler. I go through each argument and stop once I run into an error. If I can guess what the author meant to say, I throw a warning (i.e. take off points) but continue reading; otherwise, I crash (i.e. mark the proof wrong).
So by a compilation error, I just mean an error in which the student had an argument which is probably valid in their heads, but when they wrote it down, they mixed up quantifiers, used an undefined term, wrote something syntactically invalid, or similar. I believe that these are the most common errors. Here are some examples of sentences in proofs that I would consider as committing a compilation error:
For a conic section 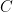 ,
, 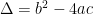 .
.
Here the variable  are undefined at the time that they are used, while the variable
are undefined at the time that they are used, while the variable  is never used after it is bound. From context, I can guess that
is never used after it is bound. From context, I can guess that  is supposed to be the discriminant of
is supposed to be the discriminant of 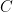 , and
, and 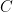 is supposed to be the conic section in the
is supposed to be the conic section in the  -plane cut out by the equation
-plane cut out by the equation 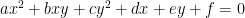 where
where 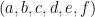 are constants. So this isn’t too egregious but it is still an error, and in more complicated arguments could potentially be a serious issue.
are constants. So this isn’t too egregious but it is still an error, and in more complicated arguments could potentially be a serious issue.
There’s another thing problematic about this example. We use “For” without a modifier “For every” or “For some”. Does just one conic section satisfy the equation 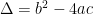 , or does every conic section satisfy this equation? Of course, the author meant that every conic section satisfies this equation, and in fact probably meant this equation to be a definition of
, or does every conic section satisfy this equation? Of course, the author meant that every conic section satisfies this equation, and in fact probably meant this equation to be a definition of 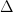 . So this compilation error can be fixed by instead writing:
. So this compilation error can be fixed by instead writing:
Let 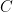 be the conic section in the
be the conic section in the  -plane defined by the equation
-plane defined by the equation 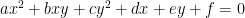 . Then let
. Then let 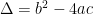 be the discriminant of
be the discriminant of 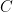 .
.
Here’s another compilation error:
Let  be a
be a  -dimensional vector space. For every
-dimensional vector space. For every 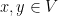 , define
, define  .
.
Here the author probably means that 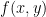 is the cross-product, or the wedge product, or the polynomial product, or the tensor product, or some other kind of product, of
is the cross-product, or the wedge product, or the polynomial product, or the tensor product, or some other kind of product, of 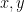 . But we don’t know which product it is! Indeed,
. But we don’t know which product it is! Indeed,  is just some three-dimensional vector space, so it doesn’t come with a product structure. We could fix this by writing, for example:
is just some three-dimensional vector space, so it doesn’t come with a product structure. We could fix this by writing, for example:
Let  , and for every
, and for every 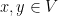 , define
, define  for the cross product of
for the cross product of 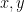 .
.
We have seen that compilation errors are usually just caused by sloppiness. That doesn’t mean that compilation errors can’t point to a more serious problem with one’s proof — they could, for example, obscure a key step in the argument which is actually fatally flawed. Arguably, this is the case with Shinichi Mochizuki’s infamous incorrect proof of Szpiro’s Conjecture. However, I think that most beginners can avoid compilation errors by making sure that they define every variable before using it, are never ambiguous about if they mean “for every” or “for some”, and otherwise just being very careful in their writing. And beginners should avoid using symbol-soup whenever possible, in favor of the English language. If you ever write something like
Suppose that  .
.
I will probably take off points, even though I can, in principle, parse what you’re trying to say. The reason is that you could just as well write
Suppose that  is a function, and for every
is a function, and for every 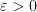 we can find a
we can find a  such that for any
such that for any  such that
such that  ,
,  .
.
which is much easier to read.
Edge-case errors. An edge-case error is an error in a proof, where the proof manages to cover every case except for a single special case where the proof fails. These errors are also often caused by sloppiness, but are more likely to actually be a serious flaw in an argument than a compilation error. They also tend to be a lot harder to detect than compilation errors. Here’s an example:
Let 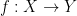 be a function. Then there is some
be a function. Then there is some  in the image of
in the image of  .
.
Do you see the problem? Don’t read ahead until you try to find it for a few minutes.
Okay, first of all, if you read ahead without trying to find the problem, shame on you; second of all, if you’ve written something like this, don’t feel shame, because it’s a common mistake. The issue, of course, is that  is allowed to be the empty set, in which case
is allowed to be the empty set, in which case  is the infamous empty function into
is the infamous empty function into  .
.
Most of the time the empty function isn’t too big of an issue, but it can come up sometimes. For example, the fact that the empty function exists means that arguably 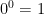 , which is problematic because it means that the function
, which is problematic because it means that the function 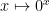 is not continuous (since if
is not continuous (since if  then
then 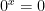 ).
).
Here’s an example from topology:
Let  be a connected space and let
be a connected space and let  . Then let
. Then let 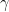 be a path from
be a path from 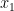 to
to 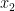 .
.
In practice, most spaces we care about are quite nice — manifolds, varieties, CW-complexes, whatever. In such spaces, if they are connected we can find a path between any two points. However, this is not true in general, and the famous counterexample is the topologist’s sine curve. The point is that it’s very important to make sure you get your assumptions right — if you wrote this in a proof there’s a good chance it would cause the rest of the argument to fail, unless you had an additional assumption that the space  did in fact have the property that connected implied path-connected.
did in fact have the property that connected implied path-connected.
In general, a good strategy to avoid errors like the above error is to beware of the standard counterexamples of whatever area of math you are currently working in, and make sure none of them can sneak past your argument! One way to think about this is to imagine that you are Alice, and Bob is handing you the best counterexamples he can find for your argument. You can only beat Bob if you can demonstrate that none of his counterexamples actually work.
Let me also give an example from my own work.
Let  be a bounded subset of
be a bounded subset of 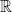 . Then the supremum of
. Then the supremum of  exists and is an element of
exists and is an element of 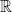 .
.
It sure looks like this statement is true, since 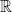 is a complete order. But in fact,
is a complete order. But in fact,  could be the empty set, in which case every real number is an upper bound on
could be the empty set, in which case every real number is an upper bound on  and so
and so 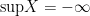 . In most cases, the reaction would be “So what? It’s just an edge case error.” But actually, in my case, I later discovered that the thing I was trying to prove was only interesting in the case that
. In most cases, the reaction would be “So what? It’s just an edge case error.” But actually, in my case, I later discovered that the thing I was trying to prove was only interesting in the case that  was the empty set, in which case this step of the argument immediately fails. A month later, I’m still not sure what to do to get around this issue, though I have some ideas.
was the empty set, in which case this step of the argument immediately fails. A month later, I’m still not sure what to do to get around this issue, though I have some ideas.
Fatal errors. These are errors which immediately cause the entire argument to fail. If they can be patched, so much the better, but unlike the other two types of errors that can usually be worked around, a fatal error often cannot be repaired.
The most common fatal error I see in beginners’ proofs is the circular argument, as in the below example:
We claim that every vector space is finite-dimensional. In fact, if 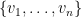 is a basis of the vector space
is a basis of the vector space  , then
, then  , which proves our claim.
, which proves our claim.
If you read a standard textbook on linear algebra, they will certainly assume that given a vector space  , you can find a basis
, you can find a basis 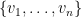 of
of  . But in fact, such a finite basis only exists if, a priori,
. But in fact, such a finite basis only exists if, a priori,  is finite-dimensional! So all the student here has managed to prove is that if
is finite-dimensional! So all the student here has managed to prove is that if  is a finite-dimensional vector space, then
is a finite-dimensional vector space, then  is a finite-dimensional vector space… not very interesting.
is a finite-dimensional vector space… not very interesting.
(This is not to say that there are almost-circular arguments which do prove something nontrivial. Induction is a form of this, as is the closely related “proof by a priori estimate” technique used in differential equations. But if one looks closely at these arguments they will see that they are not, in fact, circular.)
The other kind of fatal error is similar: there’s some sneaky assumption used in the proof, which isn’t really an edge case assumption. I have blogged about an insidious such assumption, namely the continuum hypothesis. In general, these assumptions often are related to edge-case issues, but may even happen in the generic case, as you mentally make an assumption that you forget to keep track of. Here is another example, also from measure theory:
Let  be a Banach space and let
be a Banach space and let ![F: [0, 1] \to X](https://s0.wp.com/latex.php?latex=F%3A+%5B0%2C+1%5D+%5Cto+X&bg=ffffff&fg=000000&s=0&c=20201002) be a bounded measurable function. Then we can find a sequence
be a bounded measurable function. Then we can find a sequence  of simple measurable functions such that
of simple measurable functions such that 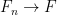 almost everywhere pointwise and
almost everywhere pointwise and  is Cauchy in mean, so we define
is Cauchy in mean, so we define  .
.
This definition looks like the standard definition of an integral in any measure theory course. However, without a stronger assumption on  , it’s just nonsense. For one thing, we haven’t shown that the definition of
, it’s just nonsense. For one thing, we haven’t shown that the definition of  doesn’t depend on the choice of
doesn’t depend on the choice of  . That can be fixed. What cannot be fixed is that
. That can be fixed. What cannot be fixed is that  might not exist at all! This happens if
might not exist at all! This happens if  is not separable, in which case the definition of the integral is nonsense.
is not separable, in which case the definition of the integral is nonsense.
This sort of fatal error is particularly tricky to deal with when one is first learning a more general version of a familiar theory. Most undergraduates are familiar with linear algebra, and the fact that every finite-dimensional vector space has a basis. In particular, every element of a vector space can be written uniquely in terms of a given basis. So when one first learns about finite abelian groups, they might be tempted to write:
Let  be a finite abelian group, and let
be a finite abelian group, and let 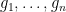 be a minimal set of generators of
be a minimal set of generators of  . Then for every
. Then for every 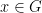 there are unique
there are unique 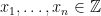 such that
such that  .
.
In fact, the counterexample here is 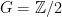 ,
, 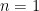 ,
, 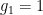 , and
, and  , because we can write
, because we can write 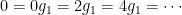 . So, when generalizing a theory, one does need to be really careful that they haven’t “imported” a false theorem to higher generality! (There’s no shame in making this mistake, though; I think that many mathematicians tried to prove Fermat’s Last Theorem but committed this error by assuming that unique factorization would hold in certain rings — after all, unique factorization holds in everyone’s favorite ring
. So, when generalizing a theory, one does need to be really careful that they haven’t “imported” a false theorem to higher generality! (There’s no shame in making this mistake, though; I think that many mathematicians tried to prove Fermat’s Last Theorem but committed this error by assuming that unique factorization would hold in certain rings — after all, unique factorization holds in everyone’s favorite ring 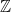 — that it fails in.)
— that it fails in.)
. We say that two smooth foliations F, G of codimension 1 in
are orthogonal if for any
, the leaves X, Y of F, G passing through p are orthogonal at p.
be a d-tuple of mutually orthogonal foliations of codimension 1 in
. Let
, let
denote the leaf of
passing through p, and let
. Then
is tangent to a principal curvature vector of
at p whenever
.
, but it was brought to my attention by Hyunwoo Kwon that there does not seem to be a good reference if
. This appears to be for superficial reasons: the usual proof is based on properties of the cross product which clearly only hold when
. I call this a superficial reason, because we can easily replace the cross product with the wedge product, and then the argument will work in general. In this blog post, I will record the proof which works for any dimension
. (Actually, it works in case
as well, but Dupin’s theorem is vacuously true in that case.)
is the intersection of
smooth hypersurfaces, each of which are mutually orthogonal and therefore are transverse. So
is a smooth curve, and its tangent space at p is a line.
such that the level sets of
are the leaves of
. Let g be the euclidean metric tensor written in the coordinates
. Orthogonality of
and
means that
. Therefore the cometric
.
, we obtain
,
,
,
,
,
. Here, the first three equations arise from the formula for the differentiated metric and the last three originate from symmetry of second partial derivatives. The only solution of this system of this equation is
for every distinct triple (i, j, k), or in other words
.
and the formula for the metric, we see that every vector in the list
. Therefore every vector in L is contained in a vector space of dimension
, but the length of L is d, so L is linearly dependent.
be the second fundamental form of
, written in the coordinate system
.
is equal to a scalar times the Hodge star of the wedge product of all of the vectors in L. Since the wedge product of L vanishes, so does
, so
is diagonal. Since the metric
on
is given by
,
is also diagonal in the coordinate system
.
is a principal curvature vector of
whenever
. But
is normal to
, so it is tangent to the curve
, as desired.